Esercizi svolti

 

Studiare la funzione $f(x)=\frac{e^{-x}}{x^2-3}$ e darne una rappresentazione grafica.

 

Dominio

Il dominio di tale funzione è $D=\left\{x\in \Re /{\text{ x}}^{\text{2}}\text{-3}\ne \text{0}\right\}=\Re -\left\{\pm \sqrt{3}\right\}.$

 

Studio del segno. Intersezioni con gli assi.

Poichè $\forall \text{x}\in D:e^{-x}>0,f\text{(}x\text{)}$ risulta positiva per $x^2-3>\mathrm{0,}$

$\text{cioè per }x\in \left]-\infty ,-\sqrt{3}\right[\cup \left]\sqrt{3},+\infty \right[$.

Si noti che, essendo $f(x)\ne 0\forall \text{x}\in D$, non ci sono intersezioni con l’asse delle ascisse.

Ricerchiamo le eventuali intersezioni con l’asse delle ordinate studiando il seguente sistema:

$\{\begin{array}{l}x=0\\ y=\frac{e^{-x}}{x^2-3}\end{array}\Rightarrow \{\begin{array}{l}x=0\\ y=-\frac{1}{3}\end{array}$

Quindi $f(x)$ interseca l’asse delle ordinate nel punto $\left(0;-\frac{1}{3}\right).$

 

Asintoti.

$\underset{x\to +\infty }{\lim }\frac{e^{-x}}{x^2-3}=0$    $\Rightarrow$    la retta $y=0$ è asintoto orizzontale destro

$\underset{x\to -\infty }{\lim }\frac{e^{-x}}{x^2-3}\stackrel{H}{=}\underset{x\to -\infty }{\lim }\frac{-e^{-x}}{2x}\stackrel{H}{=}\underset{x\to -\infty }{\lim }\frac{e^{-x}}{2}=+\infty$  $\Rightarrow$   non esistono asintoti orizzontali sinistri

$\underset{x\to -{\sqrt{3}}^{\mp }}{\lim }\frac{e^{-x}}{x^2-3}=\pm \infty$     $\Rightarrow$    la retta $x=-\sqrt{3}$ è asintoto verticale

$\underset{x\to {\sqrt{3}}^{\mp }}{\lim }\frac{e^{-x}}{x^2-3}=\mp \infty$      $\Rightarrow$    la retta $x=\sqrt{3}$ è asintoto verticale

Per trovare l’eventuale asintoto obliquo sinistro, calcoliamo:

m = $\underset{x\to -\infty }{\lim }\frac{\frac{e^{-x}}{x^2-3}}{x}=\underset{x\to -\infty }{\lim }\frac{e^{-x}}{x^3-3x}\stackrel{H}{=}\underset{x\to -\infty }{\lim }\frac{-e^{-x}}{3x^2-3}\stackrel{H}{=}\underset{x\to -\infty }{\lim }\frac{e^{-x}}{6x}\stackrel{H}{=}\underset{x\to -\infty }{\lim }\frac{-e^{-x}}{6}=-\infty$

Pertanto non esistono asintoti obliqui.

 

Monotonia. Punti di massimo e di minimo relativo.

 

$f\text{'}(x)=\frac{-e^{-x}(x^2-3)-2x{e}^{-x}}{{(x^2-3)}^2}=-\frac{e^{-x}(x^2+2x-3)}{{(x^2-3)}^2}=-\frac{e^{-x}(x+3)(x-1)}{{(x^2-3)}^2}$

Quindi:

$f\text{'}(x)>0\iff -3\text{<}x\text{<}-\sqrt{3}\vee -\sqrt{3}<x<1$

$f\text{'}(x)=0\iff x=-3\vee x=1$

$f\text{'}(x)<0\iff -\infty <x<-3\vee \text{ 1<}x\text{<}\sqrt{\text{3}}\vee \sqrt{3}<x<+\infty$

 

Dal grafico relativo al segno della derivata prima risulta chiaro che:

 

 

 

 

 

$\begin{array}{l}f(x)\text{ è crescente in (}-\mathrm{3,}-\sqrt{3}\text{) e in }(-\sqrt{3}\mathrm{,1})\\ f(x)\text{ decresce in }(-\infty ,-3),\text{ (}\mathrm{1,}\sqrt{3})\text{ e in }(\sqrt{3},+\infty )\end{array}$

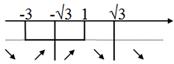
Altrettanto chiaro risulta che

$\left(-3;\frac{e^3}{6}\right)$ è punto di minimo relativo;

$\left(1;-\frac{1}{2e}\right)$ è punto di massimo relativo.

 

Grafico